I have been following the YouTube channel of the native web GmbH since my apprenticeship. I came across the channel by chance and then stuck with it because of the technical, detailed and exceptionally good videos. With the new offer of the Coding Circle, which you can unlock with a channel membership, I have decided to improve my knowledge of algorithms. The puzzles are also varied and well explained if you get stuck. You always have a week to work on the problems yourself and can also exchange ideas in the Discord and present your solutions.
Today I would like to show you my approach and my solution in Go to the Tic-Tac-Toe-Problem.
The task
Let the length of the playing field n and a list of coordinates be given. We are looking for a function that decides for a playing field of size n*n whether the coordinates contain a winning position.
Example:
n = 3
coordinates = [(0, 0), (0, 2), (1, 1), (2, 2)]
=> true
Conditions: Runtime O(n^2), Memory O(n), Single-pass.
The tests
Testing in Go is testing wonderfully simple. The standard library already comes with a lot, but I still use Testify, simply because I think it presents the assumptions more clearly.
I first create a typed collection of fields, i.e. a struct, to be able to present my test cases in a detailed and neat way. I only assume a 3*3 sized field, because this is the classic. But the code should work for other n as well, but I didn’t test that here. After that I run through all tests using a for loop and expect the achieved result to match my made assumption.
func TestHasWinningPosition(t *testing.T) {
tests := []struct {
description string
n int
input []ttt.Coordinate
expected bool
}{
{"single item in list", 3, []ttt.Coordinate{{0, 0}}, false},
{"three items in list, but no winning position", 3, []ttt.Coordinate{{0, 1}, {1, 1}, {2, 2}}, false},
{"three items in list, diagonal, left to right, winning position", 3, []ttt.Coordinate{{0, 0}, {1, 1}, {2, 2}}, true},
{"three items in list, diagonal, right to left, winning position", 3, []ttt.Coordinate{{0, 2}, {1, 1}, {2, 0}}, true},
{"three items in list, first row winning position", 3, []ttt.Coordinate{{0, 0}, {0, 1}, {0, 2}}, true},
{"three items in list, first col winning position", 3, []ttt.Coordinate{{0, 0}, {1, 0}, {2, 0}}, true},
{"four items in list, but no winning position", 3, []ttt.Coordinate{{0, 0}, {1, 1}, {2, 0}, {2, 1}}, false},
{"five items in list, but no winning position", 3, []ttt.Coordinate{{0, 0}, {0, 2}, {1, 1}, {1, 2}, {2, 1}}, false},
{"five items in list, row as winning position", 3, []ttt.Coordinate{{0, 0}, {1, 0}, {1, 1}, {1, 2}, {2, 1}}, true},
}
for _, test := range tests {
t.Run(test.description, func(t *testing.T) {
actual := ttt.HasWinningPosition(test.n, test.input)
assert.Equal(t, test.expected, actual)
})
}
}
My approach
I have imagined a classic 3*3 playing field. I represent both parties here for aesthetic reasons. However, the solution function only gets the coordinates of one party at the end.
⚪ ⚪ ⭕
⚪ ❌ ⚪
⚪ ⚪ ⚪
Eigentlich gibt es hier nur vier Möglichkeiten, die man bedenken muss:
| Horizontally | Vertically | Diagonally 1 | Diagonally 2 |
|---|---|---|---|
| ❌ ❌ ❌ ⚪ ⚪ ⚪ ⚪ ⚪ ⚪ |
❌ ⚪ ⚪ ❌ ⚪ ⚪ ❌ ⚪ ⚪ |
❌ ⚪ ⚪ ⚪ ❌ ⚪ ⚪ ⚪ ❌ |
⚪ ⚪ ❌ ⚪ ❌ ⚪ ❌ ⚪ ⚪ |
In principle, you now only have to go through the coordinates and count up a set value for each column or row. If this value reaches the size n, one has found a winning position. So in the example for “horizontal” the counter for row_0 would have the value 3.
My solution
To be able to access rows and columns more clearly, I created a struct that displays the coordinates.
type Coordinate struct {
Row int
Col int
}
So you need counter variables to determine if there is a winning position. Now you could create a counter variable for each n row and n column, but that would be either very static or very tedious. Therefore, I create a slice with length n for each row and column. For the two diagonals, of which there are always only two in each size of the game, I create two fixed counter variables.
func HasWinningPosition(n int, coordinates []Coordinate) bool {
rowCounter := make([]int, n)
colCounter := make([]int, n)
diagonalLeftToRightCounter, diagonalRightToLeftCounter := 0, 0
}
Now I iterate through the given coordinates and assign them to my local variables col and row to avoid having to handle coordinate.xy all the time. I increase the value in the row and column slice at the position of the corresponding row or column by 1. After that I compare the values of row and column. If they are the same, I know that the coordinate is on the diagonal leading from the upper left to the lower right and I increase the corresponding counter variable. If the sum of the coordinate values of row and column is equal to the size n of the playing field minus 1, the coordinate lies on the diagonal leading from top right to bottom left and I increase the value of the counter variable accordingly.
func HasWinningPosition(n int, coordinates []Coordinate) bool {
rowCounter := make([]int, n)
colCounter := make([]int, n)
diagonalLeftToRightCounter, diagonalRightToLeftCounter := 0, 0
for _, coordinate := range coordinates {
row, col := coordinate.Row, coordinate.Col
rowCounter[row]++
colCounter[col]++
if row == col {
diagonalLeftToRightCounter++
}
if row+col == n-1 {
diagonalRightToLeftCounter++
}
}
}
Finally, I just have to check if one of the count variables is equal to the playing field size due to the change. If so, a winning position is present and I return a true. If the complete list of given coordinates has been run through and thus no winning position exists, I return a false.
func HasWinningPosition(n int, coordinates []Coordinate) bool {
rowCounter := make([]int, n)
colCounter := make([]int, n)
diagonalLeftToRightCounter, diagonalRightToLeftCounter := 0, 0
for _, coordinate := range coordinates {
row, col := coordinate.Row, coordinate.Col
rowCounter[row]++
colCounter[col]++
if row == col {
diagonalLeftToRightCounter++
}
if row+col == n-1 {
diagonalRightToLeftCounter++
}
if rowCounter[row] == n || colCounter[col] == n || diagonalLeftToRightCounter == n || diagonalRightToLeftCounter == n {
return true
}
}
return false
}
The tests all run through successfully.
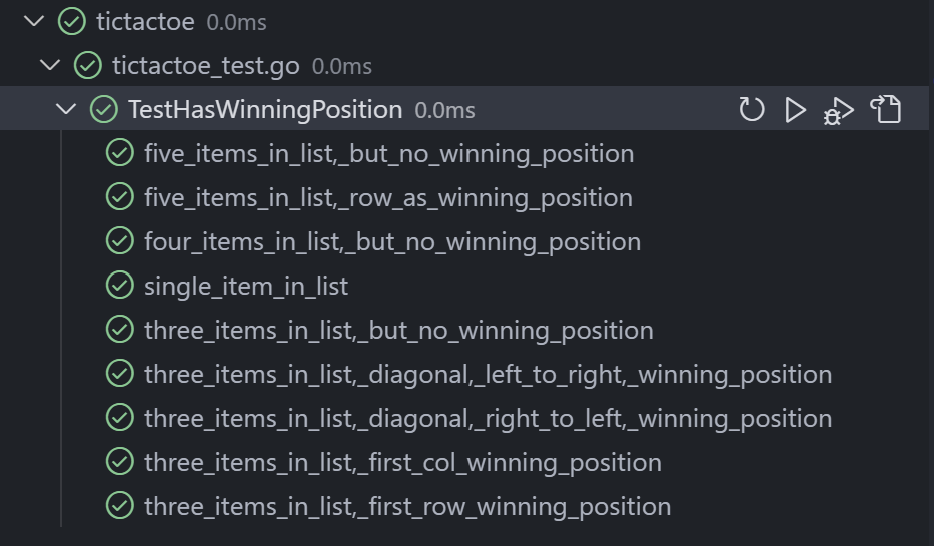
Conclusion
In solving this problem, I set out to find a good solution, not the best solution. There are certainly other approaches that may be more performant. However, in my opinion, my approach is very simple and clear and meets the requirements set. All in all, I had a lot of fun dealing with the problem and I’m already looking forward to the further tasks.
The code
You can find the code on Github. If you have any questions or comments, feel free to open an issue. I am happy about feedback.